쉐이더 짜면서 만들었던 그래프들
사이트는 이곳을 사용했다
https://www.mathway.com/ko/Graph
Mathway | 그래프 계산기
www.mathway.com
https://www.desmos.com/calculator?lang=ko
Desmos | 그래핑 계산기
www.desmos.com
로그

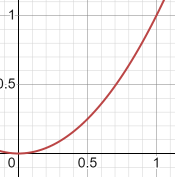
y=x*x

y=1-x*x

y=sqrt(x)

sqrt(1-x)

y=sqrt(1-abs(x))
안 쓸거 같았는데 의외로 스카이박스 쉐이더 만들때 썼다

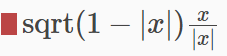
y=sqrt(1-abs(x))*x/abs(x)

y=sqrt(x)*sqrt(1-x)

y=sqrt(1-x/2)*sqrt(x*2)
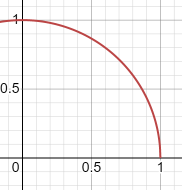

y=sqrt(1-x)*sqrt(x+1)
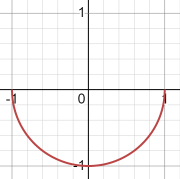
y=sqrt(x+1)*-sqrt(1-x)
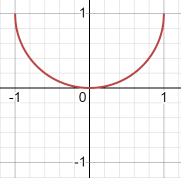
그냥 위에서 +1을 했을뿐
y=sqrt(x+1)*-sqrt(1-x)+1

y=sqrt(x+1)*sqrt(1-x)*x/abs(x)

g=(1+sqrt(5))/2 //황금비
y=(1/(x+g-1))-g+1

위공식에 1-x 했을경우
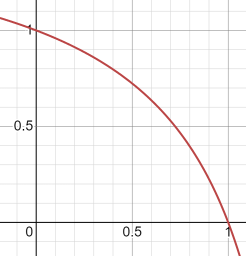

g=(1+sqrt(5))/2 //황금비
y=(1/(x-g))+g
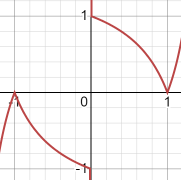

g=(1+sqrt(5))/2 //황금비
y=abs((1/(abs(x)-g))+g)*x/abs(x)

a=2
b=x*a-1
y=(b*abs(b))/a+1/a
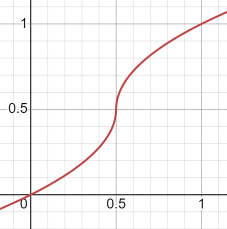
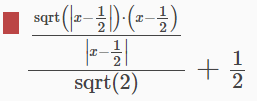
a=2
b=1/a
c=x-b
d=abs(c)
y=sqrt(d)*c/d/sqrt(2)+b
정리가 다 안되었다
일단 sqrt(2)는 앞에 sqrt안에 넣을수 있을듯
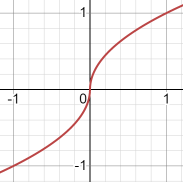
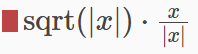
y=sqrt(abs(x))*x/abs(x)
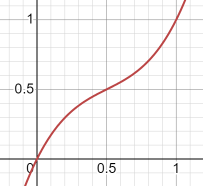
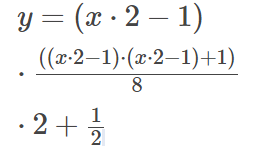
a=2
b=x*a-1
y=b*(b*b+1)/a*a+1/a
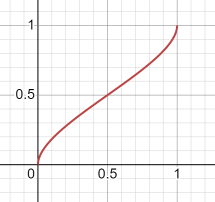
y=(sqrt(x)-sqrt(1-x)+1)/2
위와는 곡선모양이 조금 다르다
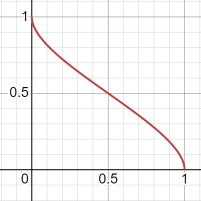
y=(sqrt(1-x)-sqrt(x)+1)/2
위에걸 좌우 뒤집음

y=x*x-x+1
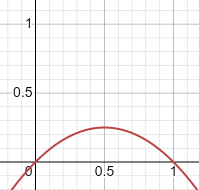
y=-(x*x-x)

y=pow(x,1/x)

y=sqrt((x-0.5)*0.5/(x*x))
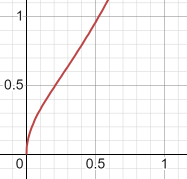
y=x*x+sqrt(x)
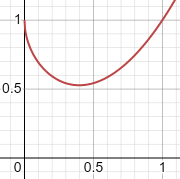
y=x*x-sqrt(x)+1
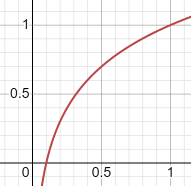
y=log(x)+1

y=log(x)*log(x)

y=(log(x)+1)*0.9
대각선 대칭처럼 보이지만 대칭은 아니다
특수한 함수들

sqrt(x*-x*x*-x) = x*x는 동일하다
동일해서 그래프가 겹치다보니 식별하기 쉽게 위의 파란색은 x*-x 로 했다
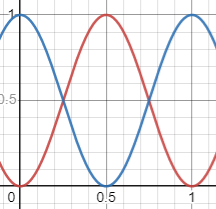
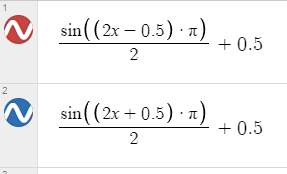
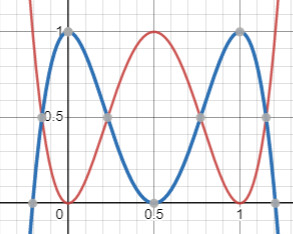
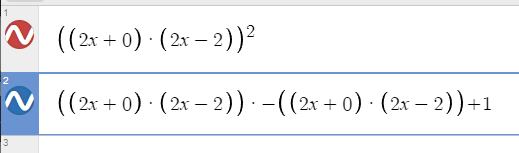

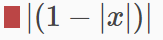
y=abs(1-abs(x))
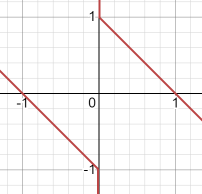
y=-x+x/abs(x)

태그: 수학
'Unity > shader' 카테고리의 다른 글
| 유니티 스카이박스 관련 (0) | 2023.01.16 |
|---|---|
| Decal Shader (0) | 2022.01.13 |
| shader pixel broken (0) | 2022.01.12 |


















